Contents

Reward

  • A reward R_t is a scalar feedback signal. Often, R_t \in \mathbb{R} or R_t \in \mathbb{Z}.

  • Indicates how well agent is doing at step t.

  • The agent’s job is to maximize cumulative reward.

Reinforcement Learning is based on the reward hypothesis

Reward Hypothesis

All goals can be described by the maximisation of expected cumulative reward.

\[max \, \mathbb{E} \left[ \sum_{i = 0}^{\infty} R_{t+i+1} \right]\]

Our goal is to sequentially perform actions which maximize expected cumulative reward.

However,

  • Any action may have long-term consequences.

  • Reward may be delayed.

  • It may be better to sacrifice immediate reward to gain greater long-term reward.

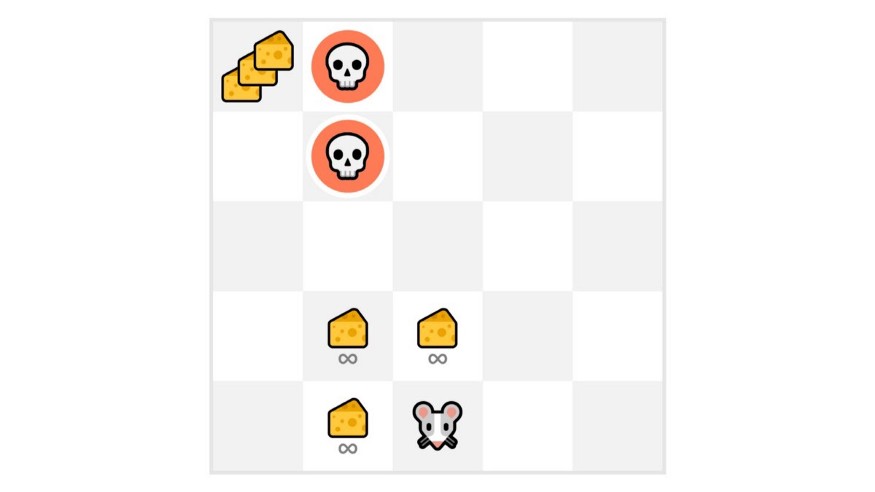
../_images/RL_example_mouse_cheese.jpg

Fig. 10 Short-term vs Long-term reward trade-off

Examples:

  1. A financial investment (may take months to mature).

  2. Refueling a helicopter (may prevent future crash).

  3. Blocking opponent moves in chess (may improve chances of winning).

Note

A RL agent’s learning process is heavily linked with the reward distribution over time, however, there is no predefined way on how to design the best reward function.

Tip: Be careful what you wish for, for you might get it

The reward function learns towards a policy it was asked for, not what should have been asked for nor what was intended.

Discounted return

Discounted return (G_t) is the cumulative reward defined as follows

\[G_t = \sum_{i = 0}^{\infty} \gamma^i \cdot R_{t+i+1}, \quad \text{where } \gamma \in \left[ 0, 1 \right]\]

  • \gamma \longrightarrow Discount rate Discount rate

  • Larger \gamma \implies Smaller discount. Agent cares more about long-term reward.

  • Smaller \gamma \implies Larger discount. Agent cares more about short-term reward.

Task-dependent discounting

Episodic Task:

  • Tasks that have a terminal state.

  • Problem naturally breaks into episodes.

  • The return becomes a finite sum.

Continuing Task:

  • Tasks that have no terminal state but can go on infinitely until stopped.

  • Problem lacks a natural end.

  • The return should be discounted to prevent absurdly large numbers.

Two ways of calculating return

  1. Batch Learning
    \[G_t = \sum_{i = 0}^{\infty} \gamma^i \cdot R_{t+i+1}\]
  2. Online Learning
    \[G_{t} = R_{t+1} + G_{t+1}\]